Методические рекомендации по использованию информационных технологий на практических занятиях

и составим определитель

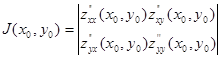
для каждой стационарной точки.

1) Для точки

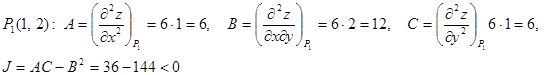
Значит, в точке экстремума нет.

2)

.

В точке , согласно достаточному условию существования экстремума, функция имеет минимум. Минимум этот равен значению функции при .

3)

.

Экстремума в точке нет.

4)

.

В точке функция имеет максимум: .

После выполнения примера необходимо ответить на вопросы студентов.

Затем предложить студентам на выбор выполнение следующих заданий. Эти задания необходимо выполнить в аудитории. Те примеры, которые не успевают решить, задаются на дом. Эти задания позволят освоить новый материал и закрепить полученные навыки. При выполнении этих заданий, так же как и в предыдущем примере, рекомендуется разбивать задания и привлекать к решению одного задания как минимум двух студентов. Это позволяет вовлечь в непосредственное изучение темы большее количество студентов. Заставит их следить за ходом решения задания и, возможно, выявит некоторые не ясные вопросы у некоторых студентов.

Исследовать на экстремум функцию

.

Решение

1. Находим стационарные точки, в которых выполняется необходимое условие существования локального экстремума функции посредствам решения системы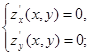

а) Находим частные производные: .

б) Составляем и решаем систему. В результате получим стационарные точки, т.е. точки подозрительные на экстремум:

,

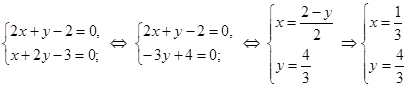таким образом, мы получили искомую стационарную точку .

2. Теперь необходимо проверить выполнение достаточного условия существования экстремума в стационарной точке, для этого необходимо найти определитель 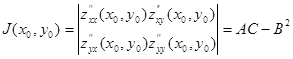, где частные производные второго порядка в стационарной точке:

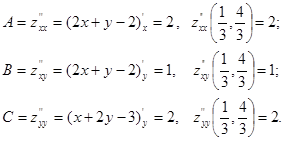
Составляем определитель:.

3. Таким образом, получили, что . Из теоремы о достаточном условии существовании экстремума можно сделать вывод, что точка является точкой локального минимума функции.

4. Найдем значение исходной функции в точке , которое является минимальным значением функции: .

Это интересно:

Физическое воспитание дошкольников в режиме здорового образа жизни
Полноценное физическое развитие и здоровье ребёнка – это основа формирования личности. В Уставе Всемирной Организации Здравоохранения (ВОЗ) говорится, что здоровье – это не только отсутствие болезней или физических дефектов, но и полное физическое, психическое и социальное благополучие. Именно поэт ...

Игра как средство нравственного воспитания у детей дошкольного возраста
Для детей от 1 до 7 лет игра – важный фактор познания окружающего мира, освоения ролевых функций, психического развития личности, её социализации и подготовки к будущему. Игра — один из видов человеческой деятельности. Как слож­ное и интересное жизненное явление, она привлекала и привле­кает вниман ...

Уровни экологизации
Экологизация является одним из общепедагогических факторов совершенствования учебно-воспитательного процесса, т.к содействует: повышению теоретического уровня преподавания благодаря взаимодействию естественно-научных и социально-гуманитарных дисциплин; формированию бескорыстных и возвышенных мотиво ...