
Учебная мотивация студента
Образование обогащает культуру, способствует взаимопониманию...

Экологическая культура
Сегодня как никогда перед человечеством стоит вопрос о необходимости...

Мониторинг ВУЗов
Мониторинг высших учебных заведений и его филиалов волнует всех жителей страны...
Методические рекомендации по использованию информационных технологий на практических занятиях
Решение
a) Первый способ (через функцию одной переменной).
1. Выразим одну переменную через другую в уравнении связи ![]() .
.
2. Подставим в исходную функцию, получили функцию одной переменной: ![]() .
.
3. Используя методику нахождения экстремума функции одной переменной, найдем первую производную функции ![]() по переменной
по переменной ![]()
![]() . Приравняем ее к нулю. Тем самым найдем стационарные точки первого рода:
. Приравняем ее к нулю. Тем самым найдем стационарные точки первого рода: ![]() . Отсюда
. Отсюда ![]() - стационарная точка 1-го рода.
- стационарная точка 1-го рода.
4. Найдем вторую производную функции ![]() , и найдем ее значение при
, и найдем ее значение при ![]() :
: ![]() , следовательно, в точке
, следовательно, в точке ![]() функция одной переменной принимает максимальное значение. Находим значение
функция одной переменной принимает максимальное значение. Находим значение ![]() из уравнения связи:
из уравнения связи: 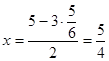 .
.
Следовательно, точка ![]() - точка максимума для исходной функции, и он равен
- точка максимума для исходной функции, и он равен ![]() .
.
б) Второй способ.
1. Рассмотрим функцию Лагранжа: ![]() .
.
2. Найдем локальный экстремум для этой функции. Для этого необходимо, используя необходимое условие существования экстремума функции, вычислить первые частные произвольные функции и решить систему, тем самым найдем стационарные точки: ![]() и составляем систему:
и составляем систему: 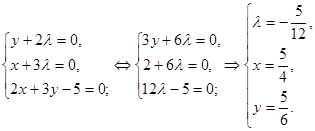
Не трудно видеть, что в точке ![]() функция
функция ![]() достигает наибольшего значения
достигает наибольшего значения ![]() .
.
Ответ: ![]() .
.
Найти наименьшее и наибольшее значения функций: ![]() в треугольнике, ограниченном прямыми
в треугольнике, ограниченном прямыми ![]() .
.
Решение
1. Изобразим эту область, это треугольник, ограниченный прямыми
Обозначим его АВС.
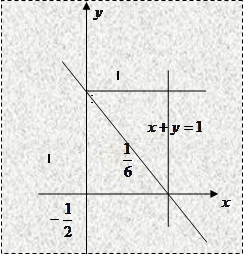
2. Найдем локальный экстремум функции ![]() .
.
Используя необходимое условие существования локального экстремума функции двух переменных, находим стационарные точки.
Находим ![]() и составляем систему:
и составляем систему:
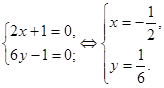
![]() - стационарная точка, и отмечая ее на графике, оцениваем принадлежность ее области АВС. Она не принадлежит области. Следовательно, она не рассматривается, так как не удовлетворяет условиям:
- стационарная точка, и отмечая ее на графике, оцениваем принадлежность ее области АВС. Она не принадлежит области. Следовательно, она не рассматривается, так как не удовлетворяет условиям:
![]() .
.
3. Исследуем функцию на границах области.
а) Рассмотрим ВС. На этой прямой переменная ![]() принимает значение 1. Подставляя значение 1 в исходную функцию, получаем функцию одной переменной и находим ее производную. Это необходимо для исследования функции на экстремум:
принимает значение 1. Подставляя значение 1 в исходную функцию, получаем функцию одной переменной и находим ее производную. Это необходимо для исследования функции на экстремум: ![]() . Приравниваем первую производную к нулю, тем самым находим точку, подозрительную на экстремум, и вычисляем значение функции в этой точке:
. Приравниваем первую производную к нулю, тем самым находим точку, подозрительную на экстремум, и вычисляем значение функции в этой точке: ![]() Точка не принадлежит области.
Точка не принадлежит области.
Это интересно:
Деятельность клубных учреждений села в организации досуга детей
Люди в деревне сильно отличаются историей своей индивидуальной жизни и выполняют так много различных функций, что делать какую-то одну функцию более существенной кажется уже не столь само собой разумеющимся. Вместо этого люди в деревне признаются как индивидуальности. Они проявляют себя в своем хар ...
Требования к обязательному уровню усвоения
содержания обучения
Тема: «Начальные геометрические сведения» Ученик должен знать: понятия отрезка, луча, угла; определение биссектрисы угла; определение и свойство смежных углов; определение и свойство вертикальных углов; определение перпендикулярных прямых. Ученик должен уметь: находить среди углов, обозначенных на ...
Эволюция традиционного воспитания в Древнем Дагестане
Проводимая в России реформа образования предполагает всесторонний учет социально-экономических и национальных особенностей развития каждого субъекта РФ и каждого народа, исследование его образовательных и воспитательных традиций. Знание этих особенностей в различные эпохи, их историко-педагогическа ...
КАТЕГОРИИ
- Главная
- Сущность, методы и этапы самовоспитания
- Методическая деятельность
- Ролевые, деловые игры
- Методика развития речи у детей
- Интегрированное изучение химии
- Диалектика воспитательного процесса
- Педагогика и воспитание
- Карта сайта

